Question

If the price is increasing at a rate of 2 dollars per month when the price is 10 dollars, find the rate of change of the demand.

Answer 1

The demand reduces by $7.12 per month

Explanation:

Given

`p\to price`

`x \to demand`

`2x^2+5xp+50p^2=24800.`

`p =10; (dp)/(dt) = 2`

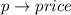
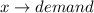
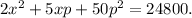
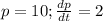
Required

Determine the rate of change of demand

We have:

`2x^2+5xp+50p^2=24800.`

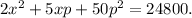
Differentiate with respect to time

`4x(dx)/(dt) + 5x(dp)/(dt) + 5p(dx)/(dt) + 100p(dp)/(dt) = 0`

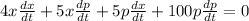
Collect like terms

`4x(dx)/(dt) + 5p(dx)/(dt) = -5x(dp)/(dt) - 100p(dp)/(dt)`

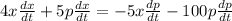
Factorize

`(dx)/(dt)(4x + 5p) = -5(x + 20p)(dp)/(dt)`

Solve for dx/dt

`(dx)/(dt) = -(5(x + 20p))/(4x + 5p)\cdot (dp)/(dt)`

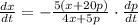
Given that:
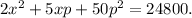`2x^2+5xp+50p^2=24800.` and
`p = 10`

Solve for x

`2x^2 + 5x * 10 + 50 * 10^2 = 24800`

`2x^2 + 50x + 5000 = 24800`

Equate to 0

`2x^2 + 50x + 5000 - 24800 =0`

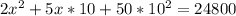
`2x^2 + 50x -19800 =0`

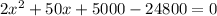
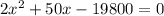
Using a quadratic calculator, we have:

`x \approx -113\ and\ x\approx88`

Demand must be greater than 0;

So:
`x=88`

So, we have:
`x=88`;
`p =10; (dp)/(dt) = 2`

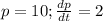
The rate of change of demand is:

`(dx)/(dt) = -(5(88 + 20*10))/(4*88 + 5*10) * 2`

`(dx)/(dt) = -(5(288))/(402) * 2`

`(dx)/(dt) = -(2880)/(402)`

`(dx)/(dt) \approx -7.16`

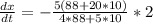
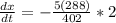
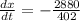
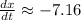
This implies that the demand reduces by $7.12 per month