Question

How many solutions does the system of equations below have?

5x + y = 8
15x + 15y = 14
no solution
one solution
infinitely many solutions

Answer 1

One solution

Explanation:

5x + y = 8

15x + 15y = 14

Lets solve using substitution, first we need to turn "5x + = 8" into "y = mx + b" or slope - intercept form

So we solve for "y" in the equation "5x + y = 8"

5x + y = 8

Step 1: Subtract 5x from both sides.

5x + y − 5x = 8 − 5x

Step 2: 5x subtracted by 5x cancel out and "8 - 5x" are flipped

y = −5x + 8

Now we can solve using substitution:

We substitute "-5x + 8" into the equation "15x + 15y = 14" for y

So it would look like this:

15x + 15(-5x + 8) = 14

Now we just solve for x

15x + (15)(−5x) + (15)(8) = 14(Distribute)

15x − 75x + 120 = 14

(15x − 75x) + (120) = 14(Combine Like Terms)

−60x + 120 = 14

Step 2: Subtract 120 from both sides.

−60x + 120 − 120 = 14 − 120

−60x = −106

Divide both sides by -60

`( -60x )/( -60 ) = ( -106 )/( -60 )`

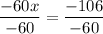
Simplify

`x = ( 53 )/( 30 )`

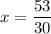
Now that we know the value of x, we can solve for y in any of the equations, but let's use the equation "y = −5x + 8"

`\mathrm{So\:it\:would\:look\:like\:this:\ y = -5 \left( ( 53 )/( 30 ) \right) +8}`

`\mathrm{Now\:lets\:solve\:for\:`

`y = -5 \left( ( 53 )/( 30 ) \right) +8}`

`\mathrm{Express\: -5 * ( 53 )/( 30 )\:as\:a\:single\:fraction}`

`y = ( -5 * 53 )/( 30 ) +8`

`\mathrm{Multiply\:-5 \:and\:53\:to\:get\:-265 }`

`y = ( -265 )/( 30 ) +8`

`\mathrm{Simplify\: ( -265 )/( 30 ) \:,by\:dividing\:both\:-265\:and\:30\:by\:5} }`

`y = ( -265 / 5 )/( 30 / 5 ) +8`

`\mathrm{Simplify}`

`y = - ( 53 )/( 6 ) +8`

`\mathrm{Turn\:8\:into\:a\:fraction\:that\:has\:the\:same\:denominator\:as\: - ( 53 )/( 6 )}`

`\mathrm{Multiples\:of\:1: \:1,2,3,4,5,6}`

`\mathrm{Multiples\:of\:6: \:6,12,18,24,30,36,42,48}`

`\mathrm{Convert\:8\:to\:fraction\:( 48 )/( 6 )}`

`y = - ( 53 )/( 6 ) + ( 48 )/( 6 )`

`\mathrm{Since\: - ( 53 )/( 6 )\:have\:the\:same\:denominator\:,\:add\:them\:by\:adding\:their\:numerators}`

`y = ( -53+48 )/( 6 )`

`\mathrm{Add\: -53 \: and\: 48\: to\: get\: -5}`

`y = - ( 5 )/( 6 )`

`\mathrm{The\:solution\:is\:the\:ordered\:pair\:(( 53 )/( 30 ), - ( 5 )/( 6 ))}`

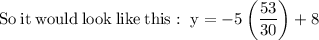
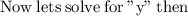
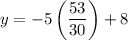
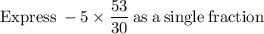
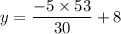
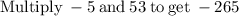
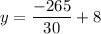
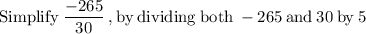
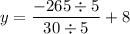
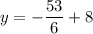
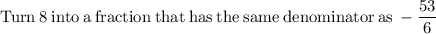
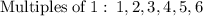
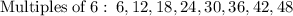
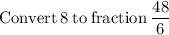
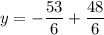
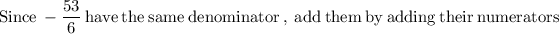
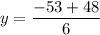
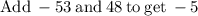
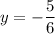
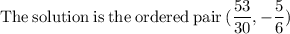
So there is only one solution to the equation.