Question

Quadrilateral WXYZ will be rotated 180° about the origin and then reflected across the Y axis. Choose all of the statements about the quadrilateral and/or the transformed quadrilateral that are correct.​

Answer 1

what the guy above me said

Explanation:

i copied his answer got it right

Answer 2

The quadrilaterals will be congruent

The quadrilateral will now appear in Quadrant 2

Explanation:

Given

`W = (-7,-2)`

`X= (-4,-2)`

`Z = (-6,-6)`

`Y =(-3,-7)`

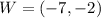
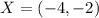
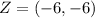
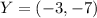
Rotation across 180 degrees

Reflection across y-axis

Required

The true statement

Using point W as a point of reference; We have:

`W = (-7,-2)`

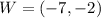
1. Rotation across 180 degrees

The rule is:

`(x,y) \to (-x,-y)`

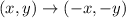
So:

`W(-7,-2) \to W'(7,2)`

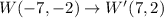
2. Reflection across y-axis

The rule is:

`(x,y) \to (-x,y)`

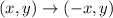
So:

`W'(7,2) \to (-7,2)`

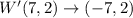
Using the above transformation on the other points; We have:

`W(-7,-2) \to W`

`X (-4,-2) \to X`

`Z (-6,-6) \to Z`

`Y(-3,-7) \to Y`

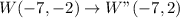
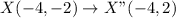
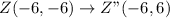
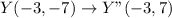
Plot the above points on a grid (see attachment).

From the grid, we can conclude that: the quadrilaterals will be congruent , and it will appear in Quadrant 2.