Question

What is the surface area of this pyramid?

Answer 1

Surface area of the given pyramid = 386.16 cm²

Explanation:

Surface area of the given pyramid = Area of the square base + Area of the lateral sides

Area of the square base = (Side)²

= (12)²

= 144 cm²

Area of the lateral side =
`(1)/(2)(\text{Base})(\text{Lateral height})`

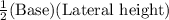
Lateral height of the triangle =
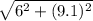`√(6^2+(9.1)^2)` [By applying Pythagoras theorem]

=
`√(82.81+36)`

=
`√(118.81)`

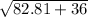
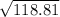
= 10.9 cm

Area of the lateral side =
`(1)/(2)(12)(10.9)`

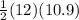
= 60.54 cm²

Surface area of the given pyramid = Area of the base + 4(Area of one lateral side)

= 144 + 4(60.54)

= 144 + 242.16

= 386.16 cm²