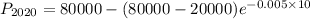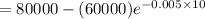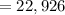Question

A community had a population of 12,000 in 1985, which is increased to 20,000 in 2010. The saturation population is 80,000. Estimate the 2020 population by (a) arithmetic growth, (b) constant percent increase, and (c) decreasing rate of increase.

Answer 1

The right answer is :

(a) 23,200

(b) 24,514

(c) 22,926

Explanation:

According to the question,

`P_1 = 12000`

`P_2 = 20000`

`P_(sat)=80000`

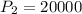
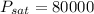
(a)

We know that the arithmetic growth formula will be:

⇒
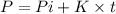`P=Pi+K* t`...(1)

here,

⇒
`K=(P_2-P_1)/(\Delta t)`

`=(20000-12000)/(25)`

`=(80000)/(25)`

`=320`

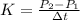
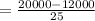
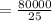
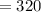
On putting the values in equation (1), we get

⇒
`P_(2020)=20000+320* 10`

`=23,200`

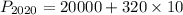
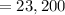
(b)

The geometric growth formula will be:

⇒
`P=ln(Pi)+K* t`

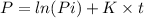
here,

⇒
`K=(lnP_2-lnP_1)/(\Delta t)`

`=(ln(20000)-ln(12000))/(25)`

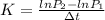
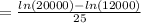
By putting the values of general log, we get

hence,

⇒
`P_f=ln(20000)+0.0204* 10`

`=10.107`

`P_(2020)=e^(10.107)`

`=24,514`

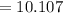
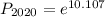
(c)

⇒
`P_f=P_(sat)-(P_(sat)-P_i)e^(-K* t)`

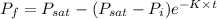
or,

⇒
`K=-(1)/(\Delta t)ln((P_(sat)-P_2)/(P_(sat)-P_1) )`

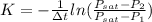
from here, we get

`=0.005`

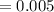
hence,

⇒
`P_(2020)=80000-(80000-20000)e^(-0.005* 10)`

`=80000-(60000)e^(-0.005* 10)`

`=22,926`