Question

A probability model includes P(red) = 27 2 7 and P(blue) = 314 3 14 . Which of the following probabilities could complete the model? Select all that apply. A. P(green) = 27 2 7 , P(yellow) = 27 2 7 B. P(green) = 38 3 8 , P(yellow) = 18 1 8 C. P(green) = 14 1 4 , P(yellow) = 14 1 4 D. P(green) = 521 5 21 , P(yellow) = 1121 11 21 E. P(green) = 37 3 7 , P(yellow) = 114 1 14

Answer 1

`(b)\ P(Green) = (3)/(8) ; P(Yellow) = (1)/(8)`

`(c)\ P(Green) = (1)/(4) ; P(Yellow) = (1)/(4)`

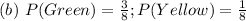
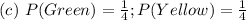
Explanation:

Given

`P(Red) = (2)/(7)`

`P(Blue) = (3)/(14)`

Required

Which completes the model

Let the remaining probability be x.

Such that:

`P(Red) + P(Blue) + x = 1`

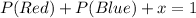
Make x the subject

`x = 1 - P(Red) - P(Blue)`

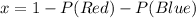
So, we have:

`x = 1 - (2)/(7) - (3)/(14)`

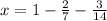
Solve

`x = (14 - 4 - 3)/(14)`

`x = (7)/(14)`

`x = (1)/(2)`

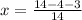
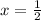
This mean that the remaining model must add up to 1/2

`(a)\ P(Green) = (2)/(7) ; P(Yellow) = (2)/(7)`

`P(Green) + P(Yellow)= (2)/(7) + (2)/(7)`

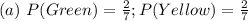
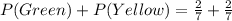
Take LCM

`P(Green) + P(Yellow)= (2+2)/(7)`

`P(Green) + P(Yellow)= (4)/(7)`

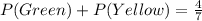
This is false because:
`(4)/(7) \\e (1)/(2)`

`(b)\ P(Green) = (3)/(8) ; P(Yellow) = (1)/(8)`

`P(Green) + P(Yellow)= (3)/(8) + (1)/(8)`

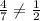
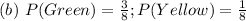
Take LCM

`P(Green) + P(Yellow)= (3+1)/(8)`

`P(Green) + P(Yellow)= (4)/(8)`

`P(Green) + P(Yellow)= (1)/(2)`

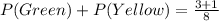
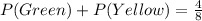
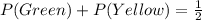
This is true

`(c)\ P(Green) = (1)/(4) ; P(Yellow) = (1)/(4)`

`P(Green) + P(Yellow)= (1)/(4) + (1)/(4)`

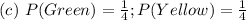
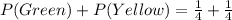
Take LCM

`P(Green) + P(Yellow)= (1+1)/(4)`

`P(Green) + P(Yellow)= (2)/(4)`

`P(Green) + P(Yellow)= (1)/(2)`

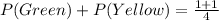
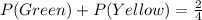
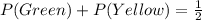
This is true

Other options are also false