Question

I know the selected answer is correct but I'm not too sure how to get that answer.

Could someone please explain.

Answer 1

√(17)/8

Explanation:

We are given with hypotenuse and base. We can have any ratio related to it, such as secant.

secA = hypotenuse/base

secA = 18/16 = 9/8

sec²A = 81/64

Using sec²A - 1 = tan²A

=> 81/64 - 1 = tan²A

=> 17/64 = tan²A

=> √(17)/8 = tanA

______________________

Using cosine of angle A.

cosA = base/hypotenuse

cos²A = (16/18) = (8/9)² = 64/81

sin²A = 1 - cos²A = 1 - 64/81 = 17/81

Hence,

tanA = √(tan²A) = √(sin²A/cos²A) = √((17/81)/(64/81)) = √(17)/8

This looks complex, either go with the 1st or one Or directly find the value of height using Pythagoras theorem,

18² = 16² + height²

√17 = height

tanA = height/base = √17/8

Answer 2

`\tt{ Hey \: there , \: Mr.Panda \: ! }` ;)

♨
`\large{ \tt{ E \: X \: P \: L \: A \: N \: A \: T \: I\: O \: N}}:`

⤻ Before solving the given question , you should know the answer of these questions :

✺How do you find the hypotenuse , perpendicular and base when the angle (
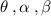`\theta \: , \alpha \: ,\beta` ) is given ?

⇾ The longest side , which is the opposite side of right angle is the hypotenuse ( h ). There are two other sides , the opposite and the adjacent. The naming of these sides depends upon which angle is involved. The opposite is the side opposite the angle involved and it is called the perpendicular ( p ) . The adjacent us the side next to the angle involved ( buy not the hypotenuse ) and it is called the base ( b ).

☄
`\large{ \tt{REMEMBER}} :`

• 
  `\bf{ \sin \theta = (opposite)/(hypotenuse) = (perpendicular)/(hypotenuse) }`

• 
  `\bf{ \cos\theta = (adjacent)/(hypotenuse) = (base)/(hypotenuse) }`

• 
  `\bf{ \tan \theta = (opposite)/(adjacent) = (perpendicular)/(base) }`

In the above cases ,
`\theta` is taken as the angle of reference.

♪ Our Q/A part ends up here! Let's start solving the question :

❈
`\large{ \tt{GIVEN}} :`

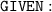
• Perpendicular ( p ) = ? , Hypotenuse ( h ) = 18 & base ( b ) = 16

✧
`\large{ \tt{TO \: FIND} : }`

• Value of tan
  `\theta`

✎
`\large{ \tt{SOLUTION}} :`

Firstly , Finding the value of perpendicular ( p ) using Pythagoras theorem :

❃
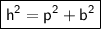`\boxed{ \sf{ {h}^(2) = {p}^(2) + {b}^(2) }}` [ Pythagoras theorem ]

`\large{ ⇢ \sf{p}^(2) + {b}^(2) = {h}^(2) }`

`\large{⇢ \sf{ {p}^(2) = {h}^(2) - {b}^(2) }}`

`\large{ ⇢\sf{ {p}^(2) = {18}^(2) - {16}^(2) }}`

`\large{⇢ \sf{ {p}^(2) = 324 - 256}}`

`\large{⇢ \sf{ {p}^(2) = 68}}`

`\large{⇢ \sf{p = √(68)}}`

`\large{ ⇢\sf{p = \boxed{ \tt{2 √(17)}} }}`

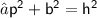
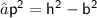
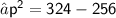
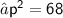
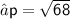
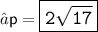
Okey, We found out the perpendicular i.e
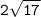`\tt{2 √(17)}` . Now , We know :

❊
`\large{ \sf{ \tan \theta} = (perpendicular)/(base) }`

`\large {\tt{↬ \: tan \theta = (2 √(17) )/(16)}}`

`\large{ \tt{ ↬ tan \theta = \frac{ \cancel{2} \: √(17) }{ \cancel{16} \: \: 8} }}`

`\large{ \tt{ ↬ \boxed{ \tt{tan \theta = ( √(17) )/(8)}}}}`

⟿
`\boxed{ \boxed{ \tt{OUR\: FINAL \: ANSWER : \boxed{ \underline{ \bf{ ( √(17) )/(8)}}}}}}`

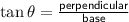
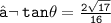
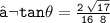
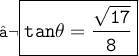
۵ Yay! We're done!

♕
`\large\tt{RULE \: OF \:SUCCESS }:`

• Never lose hope & keep on working ! ✔

ツ Hope I helped!

☃ Have a wonderful day / evening! ☼

# StayInAndExplore ☂

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁