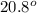Answer:
(a) PR = 55.2 cm
(b) RT = 19.7 cm
(c) <RPT =
Explanation:
(a) to determine the value of PR, apply the Pythagoras theorem to PQR.
PQ = 45, and SP = QR = 32. So that;
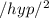 =
=
 +
+
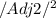
 =
=
 +
+
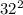
= 2025 + 1024
= 3049
PR =
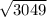
= 55.218
PR = 55.2 cm
(b) To determine RT, apply the appropriate trigonometric function to QRT.
Let RT be represented by x, so that;
Sin
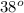 =
=

x = 32 * Sin
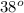
= 32 * 0.6157
x = 19.7024
RT = 19.7 cm
(c) To determine <RPT, let the angle be represented by θ.
Sin θ =
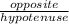
=
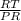
Sin θ =
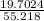
= 0.3568
θ =
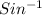 0.35568
0.35568
=
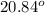
Thus, <RPT =