Answer:
(a) The energy of the photon is 1.632 x
 J.
J.
(b) The wavelength of the photon is 1.2 x
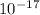 m.
m.
(c) The frequency of the photon is 2.47 x
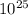 Hz.
Hz.
Step-by-step explanation:
Let;
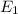 = -13.60 ev
= -13.60 ev
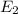 = -3.40 ev
= -3.40 ev
(a) Energy of the emitted photon can be determined as;
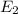 -
-
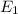 = -3.40 - (-13.60)
= -3.40 - (-13.60)
= -3.40 + 13.60
= 10.20 eV
= 10.20(1.6 x
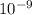 )
)
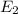 -
-
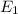 = 1.632 x
= 1.632 x
 Joules
Joules
The energy of the emitted photon is 10.20 eV (or 1.632 x
 Joules).
Joules).
(b) The wavelength, λ, can be determined as;
E = (hc)/ λ
where: E is the energy of the photon, h is the Planck's constant (6.6 x
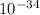 Js), c is the speed of light (3 x
Js), c is the speed of light (3 x
 m/s) and λ is the wavelength.
m/s) and λ is the wavelength.
10.20(1.6 x
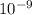 ) = (6.6 x
) = (6.6 x
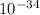 * 3 x
* 3 x
 )/ λ
)/ λ
λ =

= 1.213 x
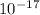
Wavelength of the photon is 1.2 x
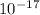 m.
m.
(c) The frequency can be determined by;
E = hf
where f is the frequency of the photon.
1.632 x
 = 6.6 x
= 6.6 x
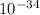 x f
x f
f =
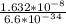
= 2.47 x
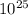 Hz
Hz
Frequency of the emitted photon is 2.47 x
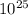 Hz.
Hz.