Question

Write 11 k-6 (2k+5)in expanded form and find the sum

Answer 1

Option B

Explanation:

Expression representing the series is,

`\sum_(k=6)^(11)(2k+5)`

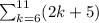
Here, k = Number of terms

By placing k = 6, 7, 8, 9, 10, 11 in the expression we can get the terms of the series.

For k = 6,

(2k + 5) = 2(6) + 5

= 17

For k = 7,

(2k + 5) = 2(7) + 5

= 19

For k = 8,

(2k + 5) = 2(8) + 5

= 21

For k = 9,

(2k + 5) = 2(9) + 5

= 23

For k = 10,

0(2k + 5) = 2(10) + 5

= 25

For k = 11,

(2k + 5) = 2(11) + 5

= 27

Therefore, expanded form will be,

17, 19, 21, 23, 25, 27

There, is a common difference in each successive to previous term,

d = 19 - 17

d = 2

Number of terms 'n' = 6

First term = 17

Sum of an arithmetic sequence is given by,

`S=(n)/(2)[2a+(n-1)d]`

Therefore, sum of the given sequence will be,

`S=(6)/(2)[2(17)+(6-1)2]`

= 3(34 + 10)

S = 132

Option B will be the correct option.