Question

A flywheel with a radius of 0.200m starts from rest and accelerates with a constant angular acceleration of 0.900rad/s2.

Compute the magnitude of the radial acceleration of a point on its rim after it has turned through 120.0.

Answer 1

The magnitude of the radial acceleration is 0.754 rad/s²

Step-by-step explanation:

Given;

radius of the flywheel, r = 0.2 m

initial angular velocity of the flywheel,
`\omega_i = 0`

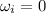
angular acceleration of the flywheel, a = 0.900 rad/s².

angular distance, θ = 120⁰

the angular distance in radian =
`(120)/(180) \pi = (2 \pi)/(3) \ rad`

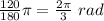
Apply the following kinematic equation to determine the final angular velocity;

`\omega _f^2 = \omega _i ^2 + 2\alpha \theta\\\\\omega _f^2 = 0 + 2(0.9)((2\pi)/(3) )\\\\\omega _f^2 = 3.7699\\\\\omega _f = √( 3.7699) \\\\ \omega _f = 1.942 \ rad/s`

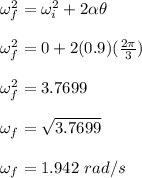
The magnitude of the radial acceleration is calculated as;

`\alpha _r = \omega ^2r\\\\\alpha _r = (1.942)^2 (0.2)\\\\\alpha _r =0.754 \ rad/s^2`

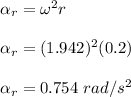
Therefore, the magnitude of the radial acceleration is 0.754 rad/s²