Question

A binomial experiment is given. Determine whether you can use a normal distribution to approximate the binomial distribution. If you can, find the mean and standard deviation. If you cannot, explain why. A survey of U.S. adults found that 37% have been to court. You randomly select 30 U.S. adults and ask them whether they have been to court.

Answer 1

Since both
`np \geq 10` and
`n(1-p) \geq 10`, you can use a normal distribution to approximate the binomial distribution.

The mean is of 11.1 and the standard deviation is of 2.64.

Explanation:

Binomial probability distribution

Probability of exactly x successes on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

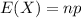
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

Using the normal distribution to approximate the binomial distribution.

This is possible if:

`np \geq 10, n(1-p) \geq 10`

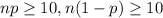
A survey of U.S. adults found that 37% have been to court. You randomly select 30 U.S.

This means that
`p = 0.37, n = 30`

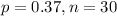
Test if it is possible:

`np = 30*0.37 = 11.1`

`n(1-p) = 30*0.63 = 18.9`

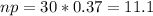
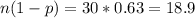
Since both
`np \geq 10` and
`n(1-p) \geq 10`, you can use a normal distribution to approximate the binomial distribution.

Mean and standard deviation:

`E(X) = np = 30*0.37 = 11.1`

`√(V(X)) = √(np(1-p)) = √(30*0.37*0.63) = 2.64`

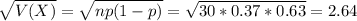
The mean is of 11.1 and the standard deviation is of 2.64.