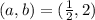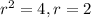Answer:
Centre:
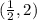
Radius =
Explanation:
General formula for a circle:
 , where
, where
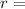 the radius of the circle and
the radius of the circle and
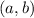 is the centre of the circle.
is the centre of the circle.
To find the centre and radius of the circle we should re-write the given equation in the form of the general formula.
So, put the terms with the same variables together:
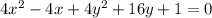
We can see that there is a common factor of
 , so let's simplify by dividing by
, so let's simplify by dividing by
 :
:
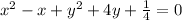
Here we can get it into the general formula by completing the square.
We do this by turning a quadratic with form
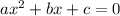 into the form
into the form
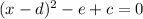 , where d is half of the coefficient of
, where d is half of the coefficient of
 , e is
, e is
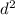 and c is the constant of the quadratic.
and c is the constant of the quadratic.
So let's re-write the equation of the circle:
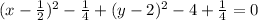
Simplify:
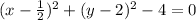
Now we can see that it's very similar to the general equation and all we have to do is bring the
 over to the right side.
over to the right side.

So, now we can find the radius and centre.