Question

An elevator has a placard stating that the maximum capacity is 1600 lb�10 passengers.​ So, 10 adult male passengers can have a mean weight of up to 1600/10=160 pounds. If the elevator is loaded with 10 adult male​ passengers, find the probability that it is overloaded because they have a mean weight greater than 160 lb.​ (Assume that weights of males are normally distributed with a mean of 166 lb and a standard deviation of 29 lb​.)

1.The probability the elevator is overloaded is?
*-Please show work to help me understand-*
2. Does this elevator appear to be​ safe?
A.Yes, there is a good chance that 10 randomly selected people will not exceed the elevator capacity.
B. No, 10 randomly selected people will never be under the weight limit.
C.Yes, 10 randomly selected people will always be under the weight limit.
D.​No, there is a good chance that 10 randomly selected people will exceed the elevator capacity.

Answer 1

1. 0.7421 = 74.21% probability the elevator is overloaded.

2. D.​No, there is a good chance that 10 randomly selected people will exceed the elevator capacity.

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

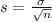For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

Assume that weights of males are normally distributed with a mean of 166 lb and a standard deviation of 29 lb​.

This means that
`\mu = 166, \sigma = 29`

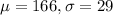
Sample of 10.

This means that
`n = 10, s = (29)/(√(10))`

1.The probability the elevator is overloaded is?

Probability that the sample mean is above 160 pounds, which is 1 subtracted by the p-value of Z when X = 160. So

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (160 - 166)/((29)/(√(10)))`

`Z = -0.65`

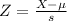
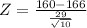
`Z = -0.65` has a p-value of 0.2579.

1 - 0.2579 = 0.7421

0.7421 = 74.21% probability the elevator is overloaded.

2. Does this elevator appear to be​ safe?

High probability of the elevator being overloaded, so not safe. Correct answer is given by option D.