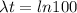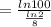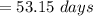Answer:
The correct answer is "53.15 days".
Step-by-step explanation:
Given that:
Half life of
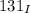 ,
,
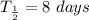
- Let the initial activity be "
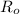 ".
". - and, activity to time t be "R".
To find t when R will be "1%" of
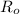 , then
, then
⇒

As we know,
⇒

or,
∴

By putting the values, we get
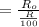
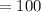
We know that,
Decay constant,
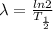
hence,
⇒