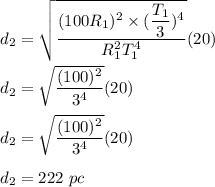Question

A main-sequence star at a distance of 20 pc is barely visible through a certain telescope. The star subsequently ascends the giant branch, during which time its temperature drops by a factor of three and its radius increases a hundredfold. What is the new maximum distance at which the star would still be visible in the same telescope?

Answer 1

Step-by-step explanation:

The surface area of a star estimated by the energy emitted per sq meter yields the overall luminosity, which can be represented mathematically as:

`L= 4 \pi R^2 \sigma T^4 --- (1)`

where;

L ∝ R²T⁴

and;

R = radius of the sphere

σ = Stefans constant

T = temperature

Also; The following showcase the relationship between flux density as well as illuminated surface area as:

`F = (L)/(A)`

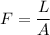
where

A = 4πd² and L ∝ R²T⁴

`F = (R^2T^4)/(4 \pi d^2) \\ \\ F \alpha (R^2T^4)/( d^2) --- (2)`

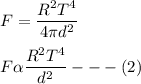
Given that:

distance d₁ = 20 pc

Then, using equation (2)

`F_1 \ \alpha \ (R^2_1T^4_1)/( d^2_1)`

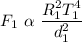
However, we are also being told that there is a temp. drop by a factor of 3;

So, the final temp.
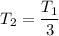`T_2 = (T_1)/(3)`; and the final radius is
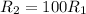`R_2 = 100R_1` since there is increment by 100 folds.

Now;

`F_2 \ \alpha \ (R^2_2T^4_2)/( d^2_2)`

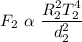
SInce;

`F_1 = F_2`

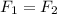
It implies that:

`(R^2_1T^4_1)/( d^2_1 ) = (R^2_2T^4_2)/( d^2_2) \\ \\ d_2 = \sqrt{(R_2^2T_2^4)/(R_1^2T_1^4)}(d_1)`

Replacing all our values, we have:

`d_2 = \sqrt{((100R_1)^2 * ((T_1)/(3))^4)/(R_1^2T_1^4)}(20 ) \\ \\ d_2 = \sqrt{((100)^2 )/(3^4)}(20 ) \\ \\ d_2 = \sqrt{((100)^2 )/(3^4)}(20 ) \\ \\ d_2 =222 \ pc`