Question

Suppose that 20% of the employees of a given corporation engage in physical exercise activities during the lunch hour. Moreover, assume that 60% of all employees are male, and 8% of all employees are males who engage in physical exercise activities during the lunch hour.

A. If we choose an employee at a random from this corporation,what is the probability that this person is a female who engages inphysical exercise activities during the lunch hour?
B. If we choose an employee at random from this corporation,what is the probability that this person is a female who does notengage in physical exercise activities during the lunch hour?

Answer 1

a) 0.152 = 15.2% probability that this person is a female who engages in physical exercise activities during the lunch hour.

b) 0.248 = 24.8% probability that this person is a female who does not engage in physical exercise activities during the lunch hour.

Explanation:

Question a:

20% of employees engage in physical exercise.

This 20% is composed by:

8% of 60%(males)

x% of 100 - 60 = 40%(females).

Then, x is given by:

`0.08*0.6 + 0.4x = 0.2`

`0.4x = 0.2 - 0.08*0.6`

`x = (0.2 - 0.08*0.6)/(0.4)`

`x = 0.38`

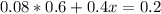
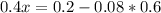
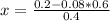
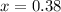
0.38 = 38%

Probability of being a female who engages in exercise:

40% are female, 38% of 40% engage in exercise. So

0.38*0.4 = 0.152

0.152 = 15.2% probability that this person is a female who engages in physical exercise activities during the lunch hour.

B. If we choose an employee at random from this corporation,what is the probability that this person is a female who does not engage in physical exercise activities during the lunch hour?

40% are female, 100% - 38% = 62% of 40% do not engage in exercise. So

0.62*0.4 = 0.248

0.248 = 24.8% probability that this person is a female who does not engage in physical exercise activities during the lunch hour.