Answer:
m∠ZWX = 105°
Explanation:
Properties of a kite,
1). One diagonal of a kite bisects at least one pair of opposite angles.
2). Diagonals of a kite kite are perpendicular to each other.
In ΔWTZ,
m∠WZT =
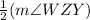
=
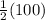
= 50°
m∠WTZ = 90° [By second property]
m∠WZT + m∠WTZ + m∠ZWT = 180°
50° + 90° + m∠ZWT = 180°
m∠ZWT = 180° - 140°
= 40°
Similarly, in ΔWTX,
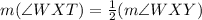
m(∠WXT) =
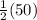
= 25°
m(∠WTX) = 90°
m∠WTX + m∠WXT + m∠TWX = 180°
90° + 25° + m∠TWX = 180°
m∠TWX = 180° - 115°
= 65°
Since, m∠ZWX = m∠ZWT + m∠TWX
Therefore, m∠ZWX = 40° + 65°
= 105°