Question

Three liquids that do not mix are poured into a cylindrical container with a diameter of 10.0 cm. The densities and volumes of the liquids are as follows.

Liquid 1: ????1 = 2.80 ✕ 103 kg/m3 and V1 = 2.00 ✕ 10−3 m3
Liquid 2: ????2 = 1.00 ✕ 103 kg/m3 and V2 = 1.50 ✕ 10−3 m3
Liquid 3: ????3 = 0.600 ✕ 103 kg/m3 and V3 = 1.00 ✕ 10−3 m3
Determine the pressure on the bottom of the container.

Answer 1

P = 9622.9 Pa = 9.62 KPa

Step-by-step explanation:

First, we will calculate the mass of all three liquids:

m = ρV

where,

m = mass of liquid

ρ = density of liquid

V = Volume of liquid

FOR LIQUID 1:

m₁ = (2.8 x 10³ kg/m³)(2 x 10⁻³ m³) = 5.6 kg

m₂ = (1 x 10³ kg/m³)(1.5 x 10⁻³ m³) = 1.5 kg

m₃ = (0.6 x 10³ kg/m³)(1 x 10⁻³ m³) = 0.6 kg

The total mass will be:

m = m₁ + m₂+ m₃ = 5.6 kg + 1.5 kg + 0.6 kg

m = 7.7 kg

Hence, the weight of the liquids will be:

W = mg = (7.7 kg)(9.81 m/s²) = 75.54 N

Now, we calculate the base area:

A = πr² = π(0.05 m)²

A = 7.85 x 10⁻³ m²

Now the pressure will be given as:

`P = (F)/(A)\\\\P = (75.54\ N)/(7.85\ x\ 10^(-3)\ m^2)`

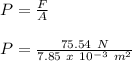
P = 9622.9 Pa = 9.62 KPa