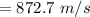Question

A hammer taps on the end of a 4.8-m-long metal bar at room temperature. A microphone at the other end of the bar picks up two pulses of sound, one that travels through the metal and one that travels through the air. The pulses are separated in time by 8.40 ms. What is the speed of sound in this metal?

Answer 1

The speed will be "872.7 m/s".

Step-by-step explanation:

As we know,

At room temperature, speed of sound will be:

e = 345 m/s

In metal bar, sound's speed will be:

=
`v>e`

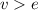
Let,

The pulse travel in time "t", then

⇒
`t=(4.8)/(v)`

⇒
`t+8.4* 10^(-3)=(4.8)/(345)`

⇒
`t+8.4* 10^(-3)=0.01391`

⇒
`t=5.5 \ ms`

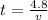
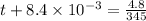
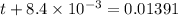
hence,

The speed of sound will be:

⇒
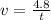
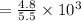
`v=(4.8)/(t)`

⇒
`=(4.8)/(5.5)* 10^3`

⇒
`=872.7 \ m/s`