Question

In ΔOPQ, the measure of ∠Q=90°, the measure of ∠O=26°, and QO = 4.9 feet. Find the length of PQ to the nearest tenth of a foot.

The length of PQ is ____ ft.

Answer 1

Given:

In ΔOPQ, m∠Q=90°, m∠O=26°, and QO = 4.9 feet.

To find:

The measure of side PQ.

Solution:

In ΔOPQ,

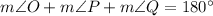`m\angle O+m\angle P+m\angle Q=180^\circ` [Angle sum property]

`26^\circ+m\angle P+90^\circ=180^\circ`

`m\angle P+116^\circ=180^\circ`

`m\angle P=180^\circ -116^\circ`

`m\angle P=64^\circ`

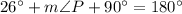
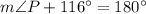
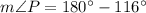
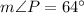
According to Law of Sines, we get

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

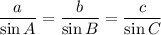
Using the Law of Sines, we get

`(p)/(\sin P)=(o)/(\sin O)`

`(QO)/(\sin P)=(PQ)/(\sin O)`

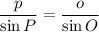
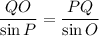
Substituting the given values, we get

`(4.9)/(\sin (64^\circ))=(PQ)/(\sin (26^\circ))`

`(4.9)/(0.89879)=(PQ)/(0.43837)`

`(4.9)/(0.89879)* 0.43837=PQ`

`2.38989=PQ`

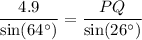
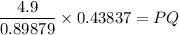
Approximate the value to the nearest tenth of a foot.

`PQ\approx 2.4`

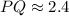
Therefore, the length of PQ is 2.4 ft.