Question

Find the TWO integers whos product is -12 and whose sum is 1

Answer 1

Explanation:

`integers \: = x \: and \: y \\ then \: x * y = - 12 ....(1)\\ x + y = 1.....(2) \\ x = 1 - y.....(3) \\ put \: (3 )\: in \: (1) \\ then \: (1 - y) * y = - 12 \\ y - {y}^(2) + 12 = 0 \\ {y}^(2) - y - 12 = 0 \\ factorise \\ {y}^(2) - 4y + 3y - 12 = 0 \\ y( y - 4) + 3(y - 4) \\ (y - 4)(y + 3) \\ y = 4 \: and \: - 3 \\ thank \: you`

Answer 2

`\rm Numbers = 4 \ and \ -3.`

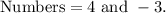
Explanation:

Given :-

• The sum of two numbers is 1 .
• The product of the nos . is 12 .

And we need to find out the numbers. So let us take ,

• First number be x
• Second number be 1-x .

According to first condition :-

`\rm\implies 1st \ number * 2nd \ number= -12\\\\\rm\implies x(1-x)=-12\\\\\rm\implies x - x^2=-12\\\\\rm\implies x^2-x-12=0\\\\\rm\implies x^2-4x+3x-12=0\\\\\rm\implies x(x-4)+3(x-4)=0\\\\\rm\implies (x-4)(x+3)=0\\\\\rm\implies\boxed{\red{\rm x = 4 , -3 }}`

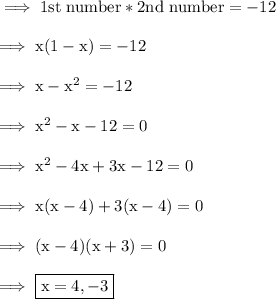
Hence the numbers are 4 and -3