Answer:
m∠B = 100°
a = 4.6
b = 7.36
Explanation:
By applying sine rule in the given triangle,
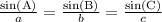
Now substitute the values in the expression,
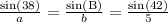
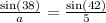
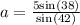
a = 4.6
By applying triangle sum theorem in ΔABC,
m∠A + m∠B + m∠C = 180°
38° + m∠B + 42° = 180°
m∠B = 180° - 80°
m∠B = 100°
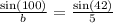
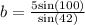
b = 7.36