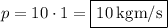Question

If a 20 N force acts on a 10 kg object for 0.5 seconds. If the object starts at rest, what would it’s new p (momentum) and v (velocity) be?

Answer 1

`p=10\:\text{kgm/s}},\\v_f=1\:\text{m/s}`

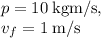
Step-by-step explanation:

From Newton's 2nd Law, we have
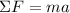`\Sigma F=ma`. We can use this to find the acceleration of object after 20 N (force) is applied to the 10 kg object.

Substituting given values, we have:

`\Sigma F=ma, \\20=10a,\\a=(20)/(10)=2\:\mathrm{m/s^2}`

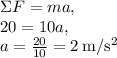
Now that we have acceleration, we can find the final velocity of object (after 0.5 seconds) using the following kinematics equation:

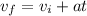`v_f=v_i+at`, where
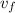`v_f` is final velocity,
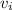`v_i` is initial velocity,
`a` is acceleration, and
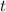`t` is time.

Solving for final velocity:

`v_f=0+2\cdot 0.5,\\v_f=\boxed{1\:\text{m/s}}`

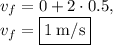
The momentum of an object is given as
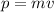`p=mv`. Since we've found the final velocity and mass stays constant, we have:

`p=10\cdot 1=\boxed{10\:\text{kgm/s}}`