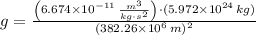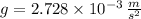Answer:
The magnitude of the free-fall acceleration at the orbit of the Moon is
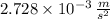 (
(
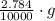 , where
, where
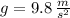 ).
).
Step-by-step explanation:
According to the Newton's Law of Gravitation, free fall acceleration (
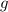 ), in meters per square second, is directly proportional to the mass of the Earth (
), in meters per square second, is directly proportional to the mass of the Earth (
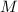 ), in kilograms, and inversely proportional to the distance from the center of the Earth (
), in kilograms, and inversely proportional to the distance from the center of the Earth (
 ), in meters:
), in meters:
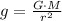 (1)
(1)
Where:
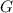 - Gravitational constant, in cubic meters per kilogram-square second.
- Gravitational constant, in cubic meters per kilogram-square second.
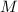 - Mass of the Earth, in kilograms.
- Mass of the Earth, in kilograms.
 - Distance from the center of the Earth, in meters.
- Distance from the center of the Earth, in meters.
If we know that
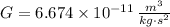 ,
,
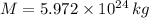 and
and
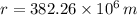 , then the free-fall acceleration at the orbit of the Moon is:
, then the free-fall acceleration at the orbit of the Moon is: