Answer:
The domain of the transformed function is the same as the parent function, but the ranges of the functions are different.
Explanation:
The domain is of the parent function is
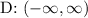 and the range is
and the range is
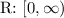 . The reflection over the x-axis and translation does not change the domain. However, the transformed function's range is
. The reflection over the x-axis and translation does not change the domain. However, the transformed function's range is
![\text{R: }(-\infty,0]](https://img.qammunity.org/2022/formulas/mathematics/high-school/d3atb2h4jnvp70vzjt0ajx8wzuavxr7ieb.png) . Therefore, the domain of the transformed function is the same as the parent function, but the ranges of the functions are different.
. Therefore, the domain of the transformed function is the same as the parent function, but the ranges of the functions are different.