Question

What is the exact value of sin
(7pie/12)

Answer 1

`\displaystyle (√(2) + √(6))/(4)`

Step-by-step explanation:

If you recall the unit circle [from the polar graph], you would have no trouble at all figuring this out, but sinse you have trouble, do not worry about it. So, here is what you should have realised:

`\displaystyle \boxed{(\pi)/(2)} = (6)/(12)\pi`

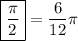
If you did not notise,
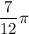`\displaystyle (7)/(12)\pi`is just
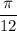`\displaystyle (\pi)/(12)`more than
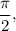`\displaystyle (\pi)/(2),`which means the exact value could possibly have a 4 in its denominatour [which obviously also has a desimal value] or could be irrational [values that cannot be written as fractions]. In this case, according to the unit circle, you will have a fraction, and that will be this:

`\displaystyle (√(2) + √(6))/(4)`

It is all about memorisation of the unit circle, which I know is difficult, but you will get used to it soon.

*Now, if you had to find
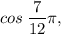`\displaystyle cos\:(7)/(12)\pi,`then the exact value would be the OPPOCITE of the exact value of
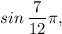`\displaystyle sin\:(7)/(12)\pi,`which is
`\displaystyle -(√(2) + √(6))/(4),`because you would be crossing into the second quadrant where the x-coordinates are negative, accourding to both the cartesian and polar graphs.

I am joyous to assist you at any time.