Note:
Ortho centre :a point of intersection of altitudes of a triangle meets the opposite angle.
Given:
For Orthocentre:.
A(1, 2), B(2, 6), C(3,-4). are vertices of a triangle:
Slope of AB[m1]=
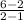 =4
=4
Since it is perpendicular to CX.
slope of CX=m2
we have for slope of perpendicular
m1m2=-1
m2=-¼
It passes through the point C(3,-4)
equation of line CX becomes;
(y-y1)=m(x-x1)
y+4=-¼(x-3)
4y+16=-x+3
x+4y+16-3=0
x+4y+13=0........[1]
again:
Slope of AC[m1]=
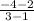 =-3
=-3
Since it is perpendicular to BY
slope of BY=m2
we have for slope of perpendicular
m1m2=-1
m2=⅓
It passes through the point B(2,6)
equation of line BY becomes;
(y-y1)=m(x-x1)
y-6=⅓(x-2)
3y-18=x-2
x-3y+18-2=0
x-3y+16=0.........[2]
Subtracting equation 1&2.
x+4y+13=0
x-3y+16=0
-__________
7y-3=0
y=

again
Substituting value of y in equation 1.
x+4*
 +13=0
+13=0
x=-13-
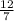
x=
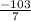 =-14
=-14

So
orthocenter is (-14
 ,
,
 )
)
And for circumcenter.
Circumcentre: a point of intersection of perpendicular bisector of the triangle.
Now
X,Y and Z are the midpoint of AB,AC and BC respectively.
X(a,b)=(
 ,
,
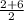 )=
)=
(
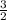 ,4)
,4)
Slope of AB=4
Slope of OX=-¼
Equation of line OX passes through (
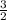 ,4)is
,4)is
y-4=-¼(x-
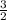 )
)
4y-16=-x+
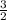
8y-16*2=-2x+3
2x+8y=3+32
2x+8y=35
x+4y=
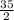 ........[1]
........[1]
again
Y(c,d)=(
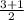 ,
,
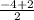 =(2,-1)
=(2,-1)
Slope of AC:-3
Slope of OY=⅓
Equation of line OY passes through (2,-1) is
y+1=⅓(x-2)
3y+3=x-2
x-3y=3+2
x-3y=5......[2]
Multiplying equation 2 by 3 and
Subtracting equation 1&2.
x+4y=35/2
x-3y=5
-_______
7y=
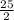
y=

Substituting value of y in equation 2.
x-3*
 =5
=5
x=5+
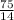
x=
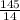
x=10
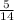
circumcenter of a triangle: (10
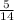 ,1
,1
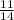 )
)