Question

Solve For w
and X
x?

Answer 1

w = 12.79

x = 5.81

Explanation:

First, solve for w:

Find the last angle of the triangle. The sum of all the angles in a triangle is

180 degrees.

A+90+52=180, this gives you angle A as 38. Use this to find w

The cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse.

Cos(B) = adj/hyp so Cos(B) = a/c rewrite as

c=10/Cos(B) or c = 10/0.61566147

c= 16.24

Now find the last side of the triangle using the Pythagorean theorem.

`a^(2) +b^(2) =c^(2) \\or\\b^(2) = c^(2) -a^(2)`

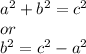
which gives you b or in this case w = 12.79

You then need w for the 2nd triangle as well as the angle 31 and the angle next to 52, which is 180-52 = 128. The other missing angle x to the triangle is 180-31-128 = 21

The law of sines is based on the proportionality of sides and angles in triangles. The law states that for the angles of a non-right triangle, each angle of the triangle has the same ratio of angle measure to sine value.

sin(x)/x=sin(B)/b=sin(C)/c

sin31/b=sin(128)/12.79 = 8.359 then

sin21/x = sin31/8.359

therefor x = 5.81