Answer:
Slope = 27/11
AB = 29.15 u
Explanation:
Given :-
- Two points are given to us .
- The points are A(7,15) and B(18,42)
To Find :-
- The slope of the line .
- The length of line AB .
We can find the slope of the line passing through the points
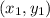 and
and
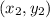 as ,
as ,
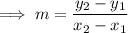
- Plug in the respective values ,
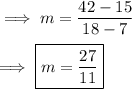
Hence the slope of the line is 27/11 .

Finding the length of AB :-
- We can find the distance between them by using the Distance Formula .

Hence the length of AB is 29.15 units .