Given:
The sum of the angles in a hexagon is 720°.
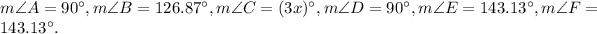
To find:
(a) Equation to solve the value of x.
(b) The value of x.
(c) The measure of angle C.
Solution:
(a)
We have,
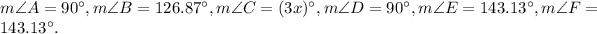
The sum of the angles in a hexagon is 720°.
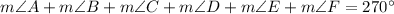
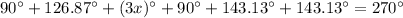
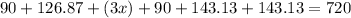
Therefore, the required equation is
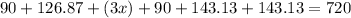 .
.
(b)
On solving the above equation, we get
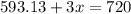
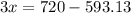
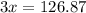
Divide both sides by 3.
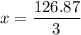
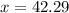
Therefore, the value of x is 42.29.
(c)
We need to find the measure of angle C.
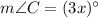

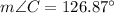
Therefore, the measure of angle C is 126.87 degrees.