Question

In Parallelogram WXYZ, diagonals WY and XZ intersect at A. WA=x2−24 and AY=2x.

What is WY?

Enter your answer in the box.

WY=
units

Answer 1

Diagonals bisect each other

• WA=AY
• x²-24=2x
• x²-2x=24
• x²-2x-24=0
• x²-6x+4x-24=0
• x(x-6)+4(x-6)=0
• (x+4)(x-6)=0

Take it positive

• x=6

Now

• AY=2(6)=12
• WY=12(2)=24

Answer 2

`\displaystyle WY = 24`

Explanation:

refer the attachment

remember that,

the diagonals of Parallelogram bisect each other so WA=AY

thus our equation is

`\displaystyle {x}^(2) - 24 = 2x`

move left hand side expression to right hand side and change its sign:

`\displaystyle {x}^(2) - 2x - 24 =0`

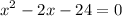
rewrite 2x and 4x-6x:

`\displaystyle {x}^(2) + 4x -6x - 24 =0`

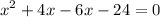
factor out x:

`\displaystyle x ({x}^{} + 4) -6x - 24 =0`

factor out -6:

`\displaystyle x ({x}^{} + 4) -6(x + 4) =0`

group:

`\displaystyle ({x}^{} + 4) (x - 6) =0`

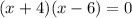
recall that,

When the product of factors equals 0 then at least one factor is 0 so

`\displaystyle \begin{cases} {x}^{} + 4 = 0 \\ x - 6 =0 \end{cases}`

`\displaystyle \begin{cases} {x}^{} = - 4\\ x =6 \end{cases}`

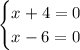
since the length cannot be negative negative x isn't available

therefore

`\displaystyle \therefore x = 6`

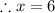
since WA and AY are the part of WY we acquire:

`\displaystyle WY = {x}^(2) - 24 + 2x`

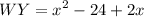
substitute the got value of x:

`\displaystyle WY = {6}^(2) - 24 + 2.6`

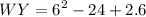
simplify square:

`\displaystyle WY = 36 - 24 + 2.6`

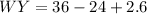
simplify multiplication:

`\displaystyle WY = 36 - 24 + 12`

simplify addition:

`\displaystyle WY = 48- 24`

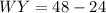
simplify substraction:

`\displaystyle WY = 24`

hence,

`\displaystyle WY = 24`