Answer:
You will have 1.585 left after 35 years.
Explanation:
Equation for amount of a substance:
The equation for the amount of a substance, using exponential decay, is given by:
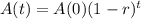
In which A(0) is the initial amount and r is the decay rate, as a decimal.
The half-life of BRADIUM-29 is 15 years.
This means that
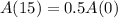 . We use this to find r.
. We use this to find r.
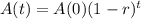
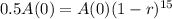
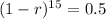
![\sqrt[15]{(1 - r)^(15)} = \sqrt[15]{0.5}](https://img.qammunity.org/2022/formulas/mathematics/college/5nrapr1wu3eaa1ncx43zwxnsiif9k39o7d.png)
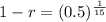
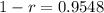
Then
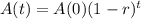
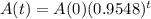
You have 8 ounces of this strange substance today
This means that
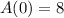 . So
. So
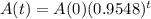
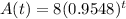
How much will you have left after 35 years?
This is A(35). So
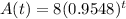
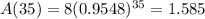
You will have 1.585 left after 35 years.