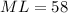Question

Find ML, JK=3x+11, ML=10x-12, NP=45

Answer 1

`ML = 58`

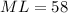
Explanation:

Given

`JK=3x+11, ML=10x-12, NP=45`

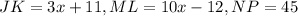
See attachment

Required

Length ML

First, calculate x using the following equivalent ratios

`JK : NP = NP : ML`

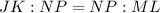
Express as fraction

`(JK )/( NP) = (NP )/( ML)`

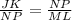
Cross Multiply

`JK * ML = NP * NP`

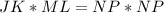
Substitute values:

`(3x +11) * (10x - 12) = 45 * 45`

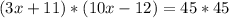
Expand

`30x^2 - 36x + 110x - 132 = 2025`

`30x^2 +74x - 132 = 2025`

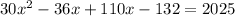
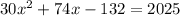
Collect like terms

`30x^2 +74x - 132 - 2025=0`

`30x^2 +74x -2157=0`

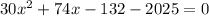
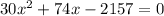
Using a calculator:

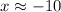`x \approx -10` and
`x \approx 7`

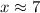
Given that:

`ML=10x-12`

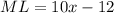
Substitute values for x

`ML=10*-10-12 = -100 - 12 = -112`

`ML=10*7-12 = 70 - 12 = 58`

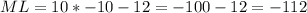
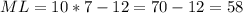
ML cannot be negative; So:

`ML = 58`