Question

Mika is a local farmer who is interested in how often residents in her town go to a farmer's market each month. She surveys 124 families and finds that, on average, those families visit a farmers' market 4.2 times per month with a sample standard deviation of 1.3. If Mika wants to be 99% confident (z=2.58) using this sample, what should her margin of error be and what does it mean?

Answer 1

The margin of error is of 0.3012, and it means that we should be 99% confident that the population mean would be within 0.3012 of the sample mean.

Explanation:

Margin of error

`M = z(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation and n is the size of the sample.

Standard deviation of 1.3

This means that
`\sigma = 1.3`

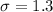
She surveys 124 families

This means that
`n = 124`

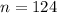
Margin of error and meaning:

`M = z(\sigma)/(√(n))`

`M = 2.58(1.3)/(√(124))`

`M = 0.3012`

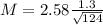
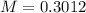
The margin of error is of 0.3012, and it means that we should be 99% confident that the population mean would be within 0.3012 of the sample mean.