Answer:
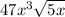
Explanation:
The objective is to combine the terms to make one radical, so therefore we know that we will have to take a
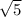 out of the second radical
out of the second radical
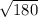 .
.
If we divide 180 by 5, we will get 36, so now we have
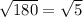 ×
×
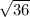
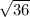 can be simplied into just 6.
can be simplied into just 6.
So now the expression becomes

Then we can further simplify by moving the
 into the radical to get two common terms with
into the radical to get two common terms with
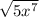 .
.
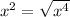 , so we now have
, so we now have
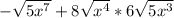
So then we can combine the two radicals to get the expression to
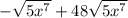
We now see that we have two terms with a common radical, and coefficients of -1, and 48.
That allows us to simplify further to
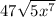
Here, we can take out
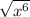 , which is
, which is
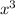 , and get the final simplied form to be
, and get the final simplied form to be
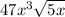
Hope this helped.