Question

Equal molar quantities of Ca2 and EDTA (H4Y) are added to make a 0.010 M solution of CaY2- at pH 10. The formation constant for CaY2- is 5.0 x 1010 and the fraction of unprotonated EDTA (Y4-) is 0.35 at pH10. Calculate the concentration of free Ca2 in this solution.

Answer 1

the concentration of free Ca2⁺ in this solution is 7.559 × 10⁻⁷

Step-by-step explanation:

Given the data in the question;

`Ca^{2+` +
`y^{4-` ⇄
`CaY^{2-`

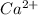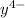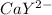
Formation constant Kf

Kf =
`CaY^{2-` / ( [
`Ca^{2+`][
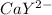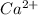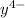`y^{4-`] ) = 5.0 × 10¹⁰

Now,

[
`y^{4-`] =
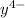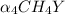`\alpha _4CH_4Y`; ∝₄ = 0.35

so the equilibrium is;

`Ca^{2+` +
`H_4Y` ⇄
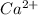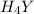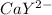`CaY^{2-` + 4H⁺

Given that;
`CH_4Y` =
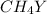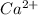`Ca^{2+` { 1 mol
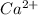`Ca^{2+` reacts with 1 mol
`H_4Y` }

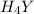so at equilibrium,
`CH_4Y` =
`Ca^{2+` = x

∴

`Ca^{2+` +
`y^{4-` ⇄
`CaY^{2-`

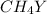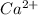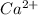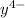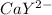
x + x 0.010-x

since Kf is high, them x will be small so, 0.010-x is approximately 0.010

so;

Kf =
`CaY^{2-` / ( [
`Ca^{2+`][
`y^{4-`] ) =
`CaY^{2-` / ( [
`Ca^{2+`][
`\alpha _4CH_4Y`] ) = 5.0 × 10¹⁰

⇒
`CaY^{2-` / ( [
`Ca^{2+`][
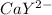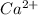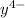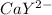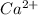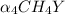`\alpha _4CH_4Y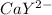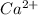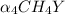`] ) = 5.0 × 10¹⁰

⇒ 0.010 / ( [x][ 0.35 × x] ) = 5.0 × 10¹⁰

⇒ 0.010 / 0.35x² = 5.0 × 10¹⁰

⇒ x² = 0.010 / ( 0.35 × 5.0 × 10¹⁰ )

⇒ x² = 0.010 / 1.75 × 10¹⁰

⇒ x² = 0.010 / 1.75 × 10¹⁰

⇒ x² = 5.7142857 × 10⁻¹³

⇒ x = √(5.7142857 × 10⁻¹³)

⇒ x = 7.559 × 10⁻⁷

Therefore, the concentration of free Ca2⁺ in this solution is 7.559 × 10⁻⁷