Question

A used car dealership surveyed 50 customers who bought a card from them two years ago. 78% of customers said that they would recommend this dealership to their friends. What is the 90% confidence interval for the percent of all former buyers who would recommend this dealership to their friends

Answer 1

The 90% confidence interval for the percent of all former buyers who would recommend this dealership to their friends is (68.36%, 87.64%).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

A used car dealership surveyed 50 customers who bought a card from them two years ago. 78% of customers said that they would recommend this dealership to their friends.

This means that
`n = 50, \pi = 0.78`.

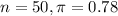90% confidence level

So
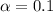`\alpha = 0.1`, z is the value of Z that has a p-value of
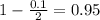`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

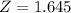The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.78 - 1.645\sqrt{(0.78*0.22)/(50)} = 0.6836`

The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.78 + 1.645\sqrt{(0.78*0.22)/(50)} = 0.8764`

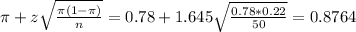
As a percent:

0.6836*100% = 68.36%

0.8764*100% = 87.64%

The 90% confidence interval for the percent of all former buyers who would recommend this dealership to their friends is (68.36%, 87.64%).