Question

1. Explain and find the volume of the round pan rounded to the nearest tenth.

2. Explain and find the volume of the rectangular pan rounded to the nearest tenth.

3. Explain how the volume of the two cake pans compare.

4. The cake density is 0.454 ounce per cubic inch and the fair price is $0.20 per ounce. What should be a fair price for each cake?

Answer 1

Step-by-step explanation:

1. Given,

Diameter of the round pan = 8in

Radius of the round pan = 8/2 = 4in

Height of the round pan = 2in

Therefore,

Volume of the round pan

`\pi {r}^(2) h`

`= 3.14 * 4in * 4in * 2in`

`= 100.48 {in}^(3)`

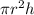
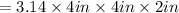
When rounded to nearest tenth,

`= 100.5 {in}^(3) (ans)`

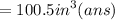
2. Given,

Dimensions of the rectangular pan = 12in, 8in, 2in

Therefore,

Volume of the rectangular pan = breadth × height × length

= 12in × 8in × 2in

`= 192 {in}^(3)`

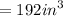
When rounded to nearest tenth,

`= 192.00 {in}^(3)`

`= 192.0 \: or \: 192 {in}^(3)`

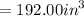
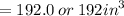
3. Volume of round pan

`= {100.5in}^(3)`

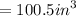
Volume of Rectangular pan

`= 192 {in}^(3)`

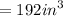
Hence,

Their difference of volume will be ,

`= (192 - 100.5) {in}^(3)`

`= 91.5 {in}^(3) (ans)`

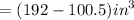
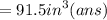
4. In this case we must know either the mass of the cake or its volume.

Given the case that we know the mass of the cake, it would be:

price = x * 0.2

where x is the mass of the cake in ounces, that is to say if for example a cake has a mass of 10 ounces, it would be:

price = 10 * 0.2 = 2

which means that each cake costs $ 2

Given the case of the volume, we must first multiply the density by this volume in order to calculate the mass and finally the price.

price = x * 0.454 * 0.2

where x is the volume of the cake in cubic inches, if for example the volume is 10 cubic inches it would be:

price = 10 * 0.454 * 0.2 = 0.908

which means that each cake costs $ 0.9