Question

The equation for line j can be written as y = 2x + 8. Another line k is perpendicular

to line j and passes through the point (6, -6). Choose the equation for line k.
Slope Intercept: y = mx + b
Point slope: (Y - Y1 ) = m (X - X1 )
A y =
1
2 – 3
2
1
y = - 2 - 3
2
B
y = -2x – 3
3
y=- 2 + 3
2

Answer 1

`\displaystyle y = - (1)/(2) x - 3`

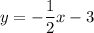
Explanation:

we are given that,

`\displaystyle E _( j): y = 2x + 8`

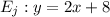
and it's perpendicular to
`E_k`

since
`E_k` is perpendicular to
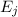`E_j` the slope of the equation of k has to be -½

because we know that

`\displaystyle m_{ \text{perpendicular}} = - (1)/(m)`

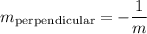
we are also given a point where the perpendicular line passes as we got the slope and a point we can consider using point-slope form of linear equation to figure out the perpendicular line

remember the point slope form

`\displaystyle y - y_(1) = m(x - x_(1))`

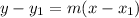
we got that, y1=-6,x1=6 and m=-½ thus,

substitute:

`\displaystyle y - ( - 6)= - (1)/(2) (x - 6)`

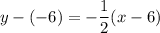
remove parentheses:

`\displaystyle y + 6= - (1)/(2) (x - 6)`

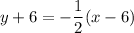
distribute:

`\displaystyle y + 6= - (1)/(2) x + 3`

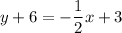
cancel 6 from both sides:

`\displaystyle y = - (1)/(2) x - 3`

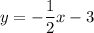
hence, the equation of line k is y=-½x-3

Answer 2

Solution given:

equation of line j is:

y=2x+8

comparing above equation with y=mx+c

we get

m=2

let slope of another line k be M

since lines are perpendicular

their product is -1

so

m *M=-1

2M=-1

M=-½

since it passes from (6,-6)

we have

(y-y1)=M(x-x1)

(y+6)=-½(x-6)

2y+12=-x+6

x+2y+12-6=0

x+2y+6=0 is a required equation of line k.