Answer:
Area of the sector = 94.25 in²
Explanation:
From the picture attached,
Length of the radius of the circle = 12 in.
m(arc BC) =

m(arc CD) =
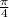
Therefore, m(arc BD) = m(arc BC) + m(arc CD)
m(arc BD) =
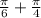
=
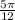
Since, area of a sector with central angle 'θ' is given by,
Area of the sector =
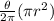
By substituting the measures in the given formula,
Area of sector BAD =
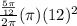
=
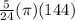
=
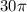
= 94.25 in²