Answer:
(a)
- Equation = 2x + 6 = 20
- Length = 13 cm
(b)
Explanation:
In the question we are given with ,
- Width of rectangle = x cm
- Length of rectangle = x + 6 cm ( Because in the question it is given that length of rectangle is 6 more than its width )
- Perimeter of rectangle = 40 cm
And we are asked to :
- Form an equation and find length.
(a) For finding equation and length ;
We know that ,
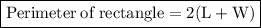
Where ,
- L = length of rectangle
- W = width of rectangle
Substituting value of length and breadth in formula and equating it with 40 to form the equation :
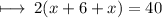
Step 1 : Solving the parenthesis :
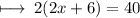
Step 2 : Dividing by 2 on both side :
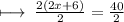
On further calculations we get :
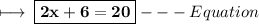
Step 3 : Subtracting 6 on both sides :

On further calculations we get :
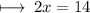
Step 4 : Dividing by 2 on both sides :
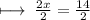
On further calculations we get :

We know that ,
- x + 6 = Length of rectangle
Henceforth ,
- Width of rectangle = 7 cm
- Length of rectangle = 7 + 6 = 13 cm
(b) For finding area of rectangle we know that ,
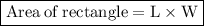
Where ,
- L = length of rectangle
- W = width of rectangle
Substituting value of length and breadth in the formula :
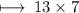

- Therefore, area of rectangle is 91 cm² .
#Keep Learning