Question

In a survey of randomly selected 3,900 family-owned businesses with revenues exceeding $1 million a year, it was found that 1,911 of them had no strategic business plan. a) Use a 90% confidence interval to estimate the proportion of family-owned businesses without strategic business plans. Give an interpretation of this interval. (5 Points) b) Would a 99% confidence interval be wider or narrower than the one you calculated in part (a)

Answer 1

a) The 90% confidence interval to estimate the proportion of family-owned businesses without strategic business plans is (0.4768, 0.5032). This means that we are 90% sure that the true proportion of all family-owned businesses without strategic business plans is between these two values.

b) Wider

Explanation:

Question a:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

In a survey of randomly selected 3,900 family-owned businesses with revenues exceeding $1 million a year, it was found that 1,911 of them had no strategic business plan.

This means that
`n = 3900, \pi = (1911)/(3900) = 0.49`

90% confidence level

So
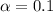`\alpha = 0.1`, z is the value of Z that has a p-value of
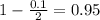`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

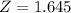The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.49 - 1.645\sqrt{(0.49*0.51)/(3900)} = 0.4768`

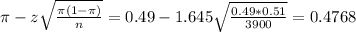
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.49 + 1.645\sqrt{(0.49*0.51)/(3900)} = 0.5032`

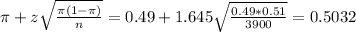
The 90% confidence interval to estimate the proportion of family-owned businesses without strategic business plans is (0.4768, 0.5032). This means that we are 90% sure that the true proportion of all family-owned businesses without strategic business plans is between these two values.

Question b:

The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

The higher the confidence level, the higher the value of z, thus the higher the margin of error and the interval is wider. Thus, a 99% confidence interval is wider than a 90% confidence interval.