Question

There are 20 people in a room, If they all shake each other's hands once and only once, HOW MANY handshakes are there altogether?

Answer 1

I thinkkkkk40 I think

Answer 2

The correct answer is option d) 190.

The number of handshakes in a room with
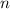`\( n \)` people can be calculated using the formula
`\( (n * (n-1))/(2) \)`. This formula accounts for the fact that each person shakes hands with every other person exactly once, and it avoids counting duplicates (e.g., the handshake between person A and person B is the same as between B and A).

For this scenario with 20 people:

`\[ \text{Number of Handshakes} = (20 * (20-1))/(2) \]`

`\[ = (20 * 19)/(2) \]`

`\[ = 10 * 19 \]`

`\[ = 190 \]`

So, there are 190 handshakes altogether.

Therefore, the correct option is (d) 190, which represents the total number of unique handshakes in the room with 20 people.