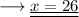Answer:
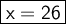
Explanation:
A right angled triangle is given to us and we need to find out the value of x . We may use Pythagoras Theorem here as ,
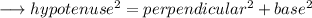
Here ,
- perpendicular = 24
- hypotenuse = x
- base = 10
On substituting the respective values , we have ;
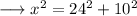
Solve the square ,
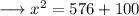
Add ,
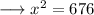
Put squareroot on both the sides ,
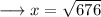
Simplify ,