Question

What is the average rate of change of f(x) = (x + 3)2 − 2

Answer 1

When we have a function f(x), the average rate of change in the interval (a, b) is:

`r = (f(b) - f(a))/(b - a)`

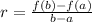
In this case, we have the function:

f(x) = (x + 3)^2 - 2

(but we do not have the interval, and I couldn't find the complete question online)

So if for example, we have the interval (2, 4)

The average rate of change will be:

`r = ((4 + 3)^2 - 2 - (2 + 3)^2 + 2)/(4 - 2) = (24)/(2) = 12`

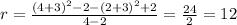
If instead, we want the rate of change in a differential dx around the value x, we need to differentiate the function (this is way more complex, so I will define some rules first).

Such that the rate of change, in this case, will be:

f'(x) = df/dx

For a function like:

g(x) = x^n + c

g'(x) = n*x^(n - 1)

And for:

h(x) = k( g(x))

h'(x) = k'(g(x))*g'(x)

So here we can write our function as:

f(x) = k(g(x)) = (x + 3)^2 - 2

where:

g(x) = x + 3

k(x) = x^2 - 2

Then:

f'(x) = 2*(x + 3)*1 = 2*x + 6

That is the rate of change as a function of x (but is not an "average" rate of change)