Question

What volume in Liters is needed to make a .99M solution with 5.3 moles of CuCl2?

Answer 1

`\boxed {\boxed {\sf 5.35 \ L}}`

Step-by-step explanation:

Molarity is a measure of concentration in moles per liter.

`molarity= (moles \ of \ solute)/(liters \ of \ solution)}`

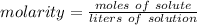
We know the molarity of the solution is 0.99 M and there are 5.3 moles of the solute, CuCl₂.

• 1 molar (M) is equal to 1 mole per liter.
• 0.99 M is equal to 0.99 moles of CuCl₂ per liter.

So,

• molarity= 0.99 mol CuCl₂/L
• moles of solute = 5.3 mol CuCl₂
• liters of solution = x (unknown)

Substitute these values into the formula.

`0.99 \ mol \ CuCl_2 / L =(5.3 \ mol \ CuCl_2)/(x)`

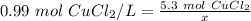
Now, solve for x by isolating the variable. First, cross multiply.

`\frac {0.99 \ mol \ CuCl_2}{1}=\frac {5.3 \ mol \ CuCl_2}{x}`

`0.99 \ mol \ CuCl_2 /L *x= 5.3 \ mol \ CuCl_2*1`

`0.99 \ mol \ CuCl_2 /L *x= 5.3 \ mol \ CuCl_2`

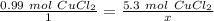
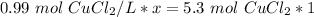
x is being multiplied by 0.99 mol CuCl₂/L. The inverse of multiplication is division. Divide both sides of the equation by 0.99 mol CuCl₂/L .

`\frac {0.99 \ mol\ CuCl_2 / L*x}{ 0.99 \ mol\ CuCl_2 \ L }=\frac {5.3 \ mol \ CuCl_2}{0.99 \ mol\ CuCl_2 \ L }`

`x=\frac {5.3 \ mol \ CuCl_2}{0.99 \ mol\ CuCl_2 \ L }`

`x=5.35353535354 \ L`

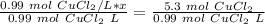
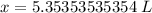
Let's round to the hundredth place. The 3 in the thousandth place tells us to leave the 5 in the hundredth place.

`x \approx 5.35 \ L`

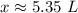
Approximately 5.35 liters are needed to make a 0.99 M solution with 5.3 moles of solute.