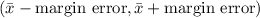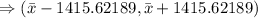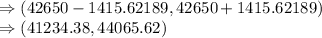Answer:
Hence, the margin error is
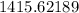 and the confidence interval for the mean is
and the confidence interval for the mean is
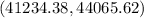 .
.
Explanation:
Given :
Sample size
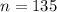
Sample mean
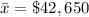
Standard deviation
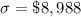
Confidence level is
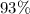
(a)
The margin error
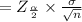
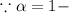 confidence level
confidence level
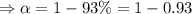
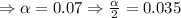
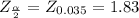 from the
from the
 table
table
Now, the margin error
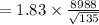
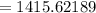
(b)
The confidence interval for the mean
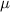 :
: