Question

A radioactive substance with initial value of 800g decays according to the exponential model A= 800e^(kt). After 10 years, only 400g of the substance remains. Find the value of k. Round your answer to the nearest thousandth. ​NO LINKS!!!!

Answer 1

k ≈ - 0.069

Explanation:

Given

A = 800
`e^(kt)`

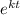
Substitute A = 400 and t = 10 into the equation

400 = 800
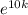`e^(10k)` ( divide both sides by 800 )

0.5 =
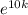`e^(10k)` ( take the ln of both sides )

ln
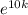`e^(10k)` = ln0.5

10k lne = ln0.5 [ lne = 1 ]

10k = ln 0.5 ( divide both sides by 10 )

k =
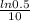`(ln0.5)/(10)` ≈ 0.069 ( to the nearest thousandth )

Answer 2

Explanation:

400 = 800 * e^(k*t)

What are the units of t? I'm taking it as years.

Divide by 800

400/800 = e^(k*10)

1/2 = e^(k*10)

ln(1/2) = ln(e)^(k*10)

ln(1/2) = k*10 * ln(e)

ln(e) = 1

-0.69314 = k*10

-0.069314 = k

Check

A = 800 e^(-0.069314*10)

A = 800 e^(-0.69314)

A = 800 * 0.50000359

A = 400.0028722

Which is close enough to 400