Question

The functions ) and g(x) are shown on the graph.

Rx) = x2
What is g(x)?
g(x) (2, 12)

Answer 1

Given:

The graphs of f(x) and g(x).

The function f(x) is given by:

`f(x)=x^2`

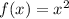
The graph of g(x) passes through the point (2,12).

To find:

The function g(x).

Solution:

From the given graph it is clear that the vertex of both function f(x) and g(x) is at (0,0). It means the graph of f(x) is not translated. It means the graph of f(x) is only vertically stretched to get the graph of g(x). So,

`g(x)=kf(x)`

Where, k is the stretch factor.

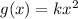`g(x)=kx^2` ...(i)

The graph of g(x) passes through the point (2,12). Putting
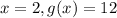`x=2, g(x)=12`, we get

`12=k(2)^2`

`12=k(4)`

`(12)/(4)=k`

`3=k`

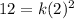
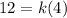
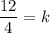
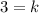
Putting
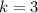`k=3` in (i), we get

`g(x)=3x^2`

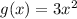
Therefore, the correct option is A.